Think Before You CONV #( )
Contents
As I have previously written, ABAP has weak static types. This means that conversions between types are easy to do, even to the point that one can unintentionally do it.
Implicit Conversions
|
|
Erlang, in contrast, has strong dynamic types and single assignments, which means that it is not possible to assign a variable of one type to a variable of another type. The only way to convert between types is to use a function that takes one type as a parameter and returns another type:
|
|
Implicitly converting between types has its upsides: simply assigning a string to an integer is much simpler than invoking a function or a method. Downsides of implicit conversions in ABAP include the fact that some statements that look like simple assignment can now crash (if the values happen to be incompatible) and also that implicit conversions can corrupt the values:
|
|
This sort of corruption also happens when converting between integers and floating-point types. Integers cannot represent the decimal part of a floating-point number, so something must be done about it. Some programming languages drop the decimal part (in effect, round it down) while others round the value to the nearest integer. Depending on the case, either one of these solutions might be acceptable.
In ABAP, the value is rounded to the nearest integer:
|
|
Rounding and omitted characters are examples of when an implicit conversion changes the value somehow. The resulting value may still be technically valid, but not what the programmer intended.
There are also cases where an implicit conversion does not do enough:
|
|
Although this implicit conversion does not corrupt the value in any way (GERNR type is 18 characters long), the value currently in lv_serial_number is still not valid. This is because GERNR has an additional requirement: if a value consists of only numbers, the value must be left-padded with zeroes so that all the 18 characters are used. When a value arrives from the user interface, this conversion would be executed by a function module. Implicit conversion, however, does not handle this step:
|
|
Various fields in ABAP (AUFNR, MATNR, DOKNR etc.) have these sorts of additional requirements. The conversion exit can be found in the domain definition of the type.
Another way that an implicit conversion can fail to do enough is when a field is defined as case-insensitive:
|
|
A UUID (or a GUID) is a string made up of 32 characters (or 36 characters, if dashes are used to structure the string). It encodes a binary value (a MAC-namespaced timestamp, a hashed value or a random value) and thus valid characters of a UUID are those used to represent hexadecimal values: 0-9 and A-F, for a total of 16 different value. Both ‘a’ and ‘A’ represent value 10, the character case is insignificant.
By default, ABAP methods that generate UUIDs return uppercase values (which is the ABAP default for case-insensitive values). Type SYSUUID_C32 is also defined to be case-insensitive. The important thing is that comparisons between UUIDs happen not according to standard character string comparison (where character case matters), but according to the logic of whether the two UUIDs (regardless of the character case), represent the same value.
However, implicit conversions just move the characters from string to the case-insensitive variable, without modifying the character case. This is one of the peculiar features of ABAP: the field is not really case-insensitive, but the metadata causes the case of the values to be normalized when they are accepted from the user interface. Technically it is still possible to store case-sensitive values in case-insensitive variables.
Class Methods Are Type-Safe
Although syntax for passing parameters to a method call resembles assignment statements where implicit conversions happen, using incompatible values produces a compilation error:
|
|
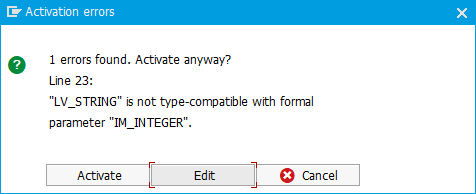
Incompatible types
Depending on the case, this is either a nice sanity check or an unnecessary hinderance. For example, if a parameter expects a string type, any char type would in theory work (since a string has no upper length limit, thus allowing it to contain any char type value).
The old way to get around this check would be define a temporary variable of the correct type. In more recent versions of ABAP, the conversion can be done without the extra variable:
|
|
Enter CONV #( ). A new ABAP operator, it takes a value of one type and converts it to the type inferred from the context (the # symbol means that some sort of type inference takes place). This allows for implicit conversions of parameters in method calls and is therefore a tool that programmers reach for when they get a compilation error caused by incompatible types.
Although this seems like a convenient solution, the previously listed caveats of implicit conversions apply here: while the result of CONV #( ) will be of the expected type and will thus technically work, the value may still be invalid.
Take for example timestamps. ABAP does not have a real timestamp type. Rather, packed numbers are used to represent timestamps.
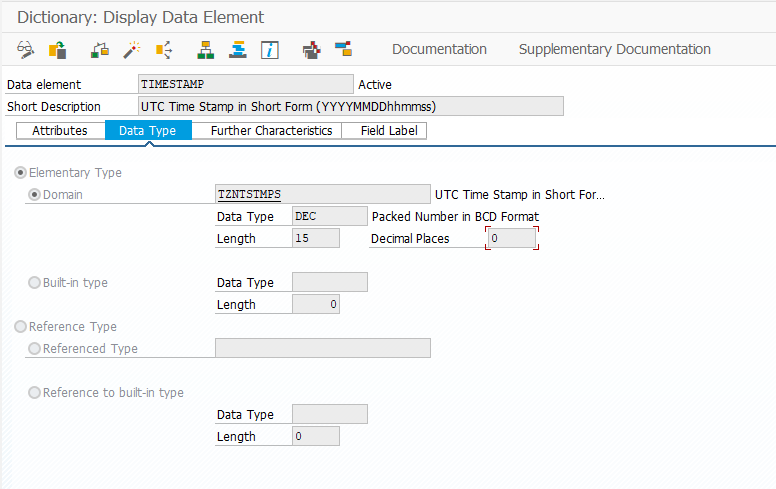
Timestamp
|
|
Unlike a UNIX timestamp (seconds since UTC 1970-01-01 00:00:00), an ABAP timestamp is simply a concatenation of an ABAP date and UTC time values, stored in a packed number variable. Unlike ABAP date values, which one can operate on using ADD and SUBTRACT statements:
|
|
ABAP timestamps really are just packed numbers and must be operated using the class CL_ABAP_TSTMP. Using ADD AND SUBTRACT might work in some cases, but would more likely just produce invalid timestamp values:
|
|
Like an ABAP time variable, the timestamp variables above are accurate to the second. There is also a “long timestamp” type which is accurate to the millisecond (or hundreds of nanoseconds):
|
|
To allow for accuracy in the sub-second range, the long timestamp type simply adds a fraction part.
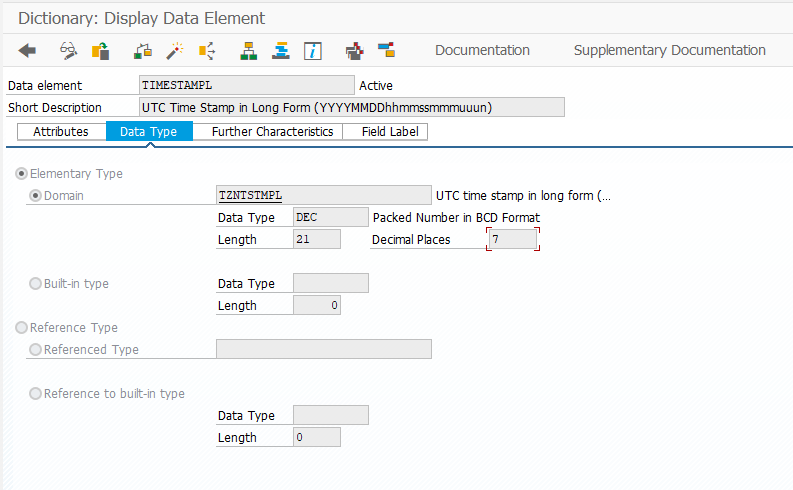
Long timestamp
Now, suppose you have a long timestamp value and a method which only accepts a normal timestamp. You will obviously use CONV #( ), right? After all, a long timestamp can represent any value that is representable by a timestamp, so in theory there is no issue. Right?
Keep in mind that a timestamp is simply a packed number. When we implicitly convert a packed number with a fraction part to a packed number without one, the value gets rounded to the nearest integer. While not ideal, the rounding that results from this may or may not be acceptable. For example, a second here or there might not matter when tracking physical events of humans. Tracking computer events, the rounding might give an incorrect idea of the order of events (though the more fundamental error would be to think that tracking computer activity on the level of seconds is accurate enough).
ABAP Timestamps, however, are special. A UNIX timestamp is simply some number of seconds that have passed since UTC 1970-01-01 00:00:00. By definition, adding a second (or a thousand) will always result in another valid UNIX timestamp: the new one is just one (or a thousand) seconds farther from UTC 1970-01-01 00:00:00 than the previous one. The same does not hold for ABAP timestamps.
For example, the next valid value after ABAP timestamp 20250202105959 is not 20250202105960, but instead 20250202110000. This means that instinctually reaching for CONV #( ) may result in corrupted values:
|
|
Implicit conversions are handy, but they also hide many potential issues from the programmer. In contrast, a method of type timestampl -> timestamp would convert between types while respecting their internal structure.
Instinctually reaching for CONV #( ) every time you get a compilation error caused by incompatible parameter types is a bad habit. While using CONV #( ) can sometimes be okay, one should always stop and think before using it. After all, static types – and the compilation errors they make possible – are there to warn to you about potential errors.