Table Types and Function Modules
Contents
I had taken arrays for granted until a programming class I attended had an exam question to the effect of “Why do programming languages have arrays?”
Even if you have not previously thought it through, the answer is fairly intuitive: arrays allow programs to generalize to inputs and problems of varying sizes.
Collection Types
Arrays, or “collection types” more generally, exist in all modern programming languages. In fact, it is likely that a programming language has an extensive catalog of collection types with different properties:
- Arrays have a fixed size, use numeric keys (indexes), allow any element to be quickly accessed but changing the size of an array is expensive because new memory needs to be allocated and the contents of the array must be copied.
- Lists are cheap to grow or shrink, but random access to members is slow.
- Sorted lists allow random members to be accessed faster, while making the addition and removal of members slower.
- Stacks are like lists, but elements are inserted and removed using Last In-First Out (LIFO) rule.
- Dictionaries (AKA maps or associative arrays) optimize for access with a known key, but enumerating over the members of the collection will happen in an undefined order.
- Ordered dictionaries preserve the fast access with a known key and add a defined order of element enumeration.
- Sets optimize for testing whether a given value is a member of the set.
Most of these collection types are generic in the sense that the properties of the collection hold regardless of the type of value they contain. Of the exceptions, sorted lists impose the obvious restriction that it must be possible to compare elements amongst themselves, and dictionaries (likely) require that the key type can be “hashed” (ie. mapped to a type that the dictionary implementation uses internally, and for which it still holds that each key value maps to a unique value of the internal type).
Because collection types are generic, they are often implemented using generics, meaning that the collection type is implemented once and then reused as required with any compatible type.
|
|
Dynamic languages may impose some restrictions on the key type of associative arrays (must be hashable, for example), but the value types are usually a free-for-all, even to the point that a collection may contain multiple different types.
|
|
ABAP, however, differs from most programming languages when it comes to collection types.
ABAP Collections
One of the distinctive features of ABAP is that the only built-in collection type is the list, which is officially called an “internal table” and which will be henceforth referred to as a “table type” in this post. (Were I forced to speculate, I would guess that the name “internal table” tries to draw a distinction between an in-memory table and a database table, which would probably be called an “external table”)
|
|
Not only that, but table type is not generic: you have to define a type for every data type you need to treat as a collection. This sounds worse than it is and does not actually differ terribly much from other programming languages. The main difference is where and how you can define the table type that you want to use.
For example, in Swift this definition happens by specifying the generic type and the type parameter:
|
|
Array<Int> works everywhere, be it declaring a variable (in any scope), parameter, member of a structure or the return value of a function.
In ABAP, you can sometimes create a table by just referring to the contained data type (as one does in languages with generic types). In other cases you must have an already defined data type available:
|
|
However, depending on how the ZINTEGER_TTY type was defined, the above may not compile:
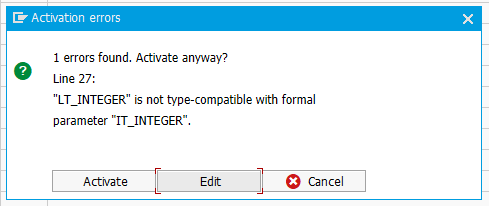
Incompatible tables
Which brings us to the topic of different types of table types.
Types of Table Types
The most obvious way that two table types could be incompatible is, of course, that the types that they contain are different. It does not make sense that a table of integers would work in places that expect a table of strings. This also applies to ABAP.
In our example, however, two tables of integers are incompatible. How can two tables containing integers still be different? The answer is that not all table types in ABAP are the same; the table type definition contains more than just the contained type:
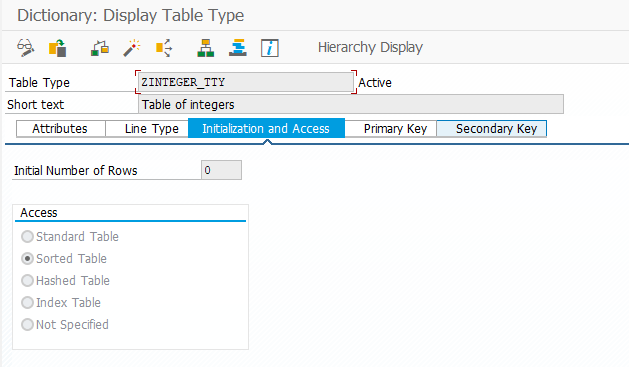
Table types
In truth, table types in ABAP can be STANDARD, SORTED or HASHED tables. These correspond roughly to a List, a Sorted List and a Dictionary; that is, the two latter options provide additional guarantees as to the order of elements and uniqueness of keys. These guarantees also cause STANDARD, SORTED and HASHED table types to be incompatible when used as parameter types: it would not make sense to allow a STANDARD table, with potentially multiple instances of the same key, to be used in a parameter that required a HASHED table, where every key only occurs once.
The next obvious question is: “Keys? Since when have Lists had keys?” And in this regard, too, ABAP is unique. Every table type in ABAP has an explicitly or implicitly defined key:
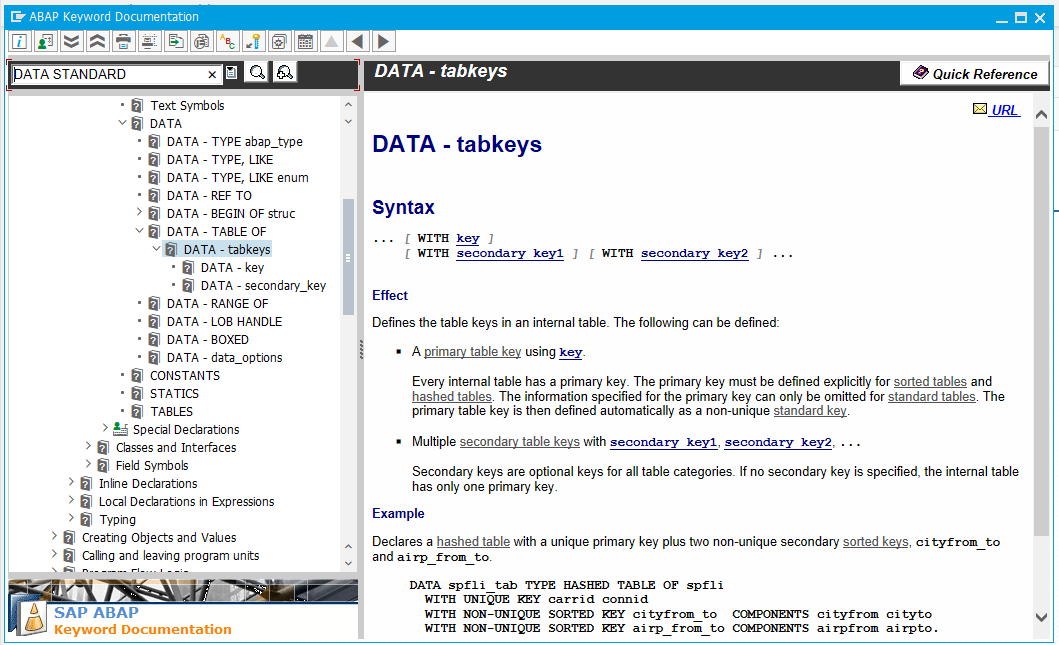
Table keys
In case you are wondering what a “standard key” could possibly mean, here is the definition:
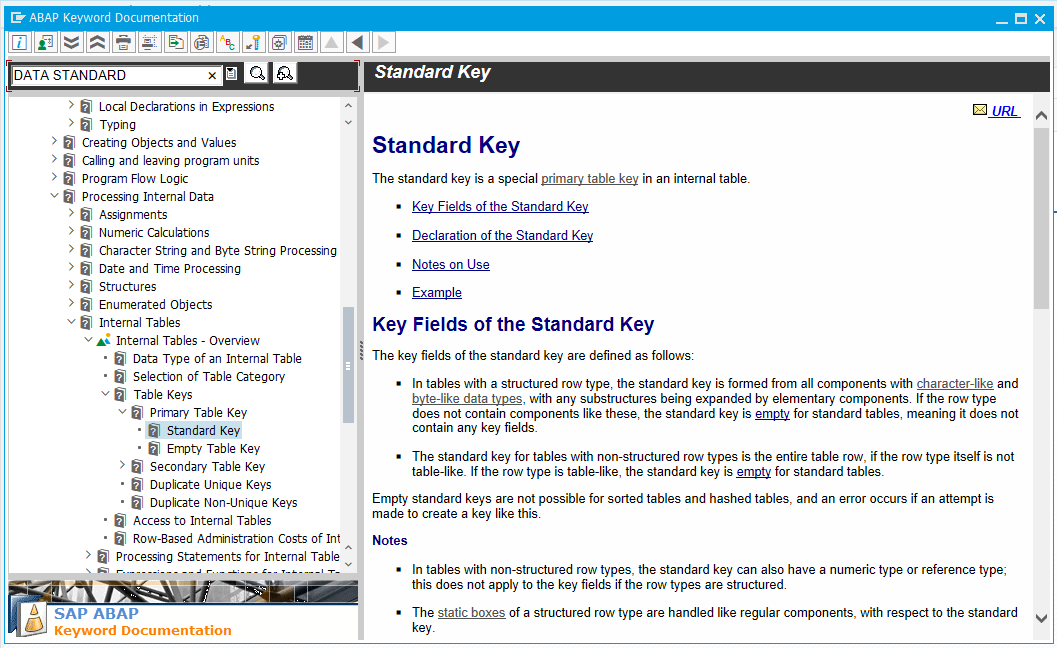
Standard key definition
The key fields of the standard key are defined as follows:
- In tables with a structured row type, the standard key is formed from all components with character-like and byte-like data types, with any substructures being expanded by elementary components. If the row type does not contain components like these, the standard key is empty for standard tables, meaning it does not contain any key fields.
- The standard key for tables with non-structured row types is the entire table row, if the row type itself is not table-like. If the row type is table-like, the standard key is empty for standard tables.
Empty standard keys are not possible for sorted tables and hashed tables, and an error occurs if an attempt is made to create a key like this.
In other words, we would have had to define our table type variable such that it was compatible with the parameter type:
|
|
Table keys can also be specified when defining the table type in ABAP dictionary:
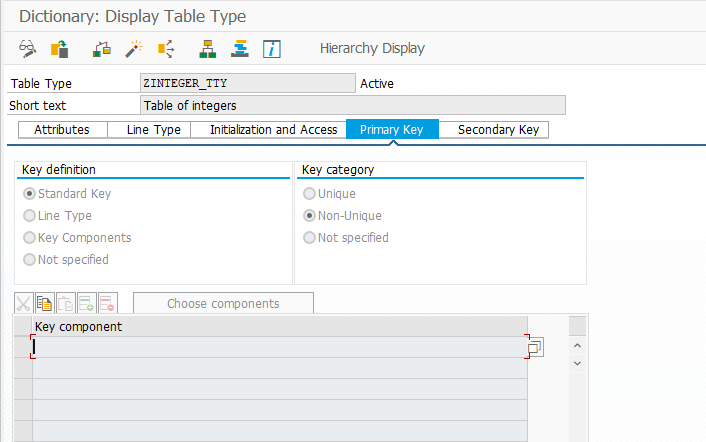
Table type primary key
The list titled “Key component” makes more sense when the table type is defined for a structure:
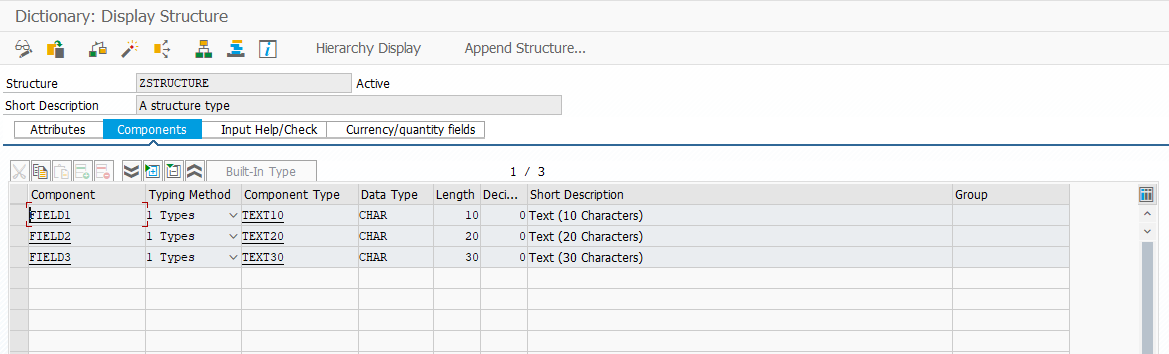
Structure type (ZSTRUCTURE)
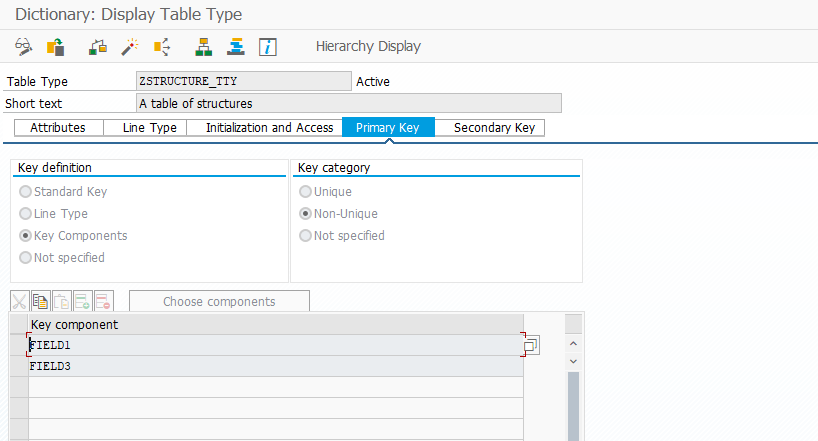
Table type for structure type (ZSTRUCTURE_TTY)
Accessing SORTED and HASHED tables by the table key should be faster than when using a STANDARD table. However, this performance gain seems to only manifest with huge tables while all three are more or less the same when the number of rows is small.
The presence of keys and the fact that programmers can decide which fields make up the key introduces another potential source for table type incompatibility. For example, if we have yet another table type with the same key fields in reverse order:
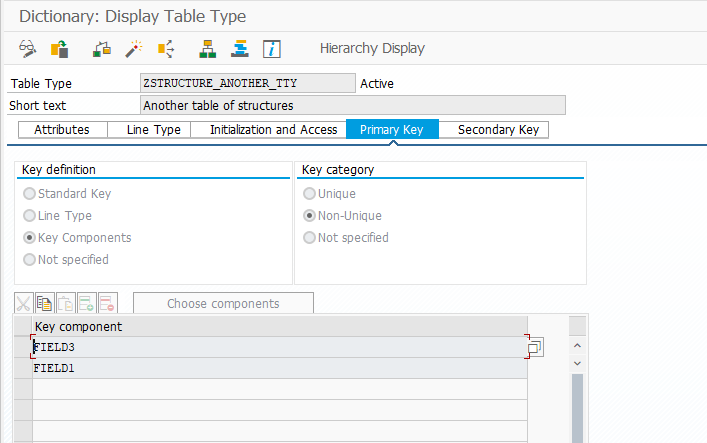
Another table type for structure type
These tables are no longer compatible:
|
|
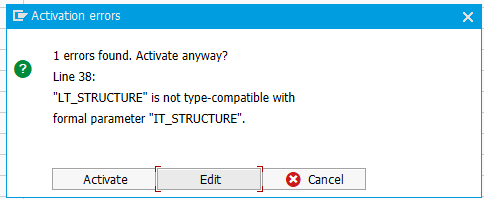
Tables with different keys are incompatible
This makes sense, since different keys imply different orders of entries in the tables. Table types with identical definitions are, however, compatible. The following table type would work anywhere where ZSTRUCTURE_ANOTHER_TTY would work:
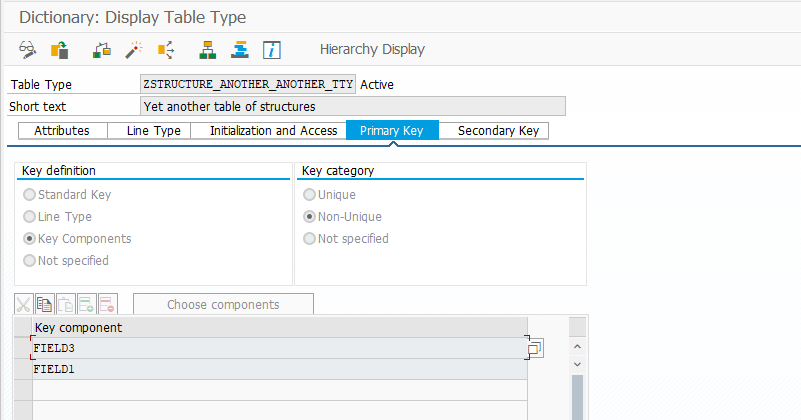
This type is compatible with ZSTRUCTURE_ANOTHER_TTY
Somewhat surprisingly, table types for identical structures with differently named components are still compatible. The following structure and table type are compatible with ZSTRUCTURE and table type ZSTRUCTURE_TTY:
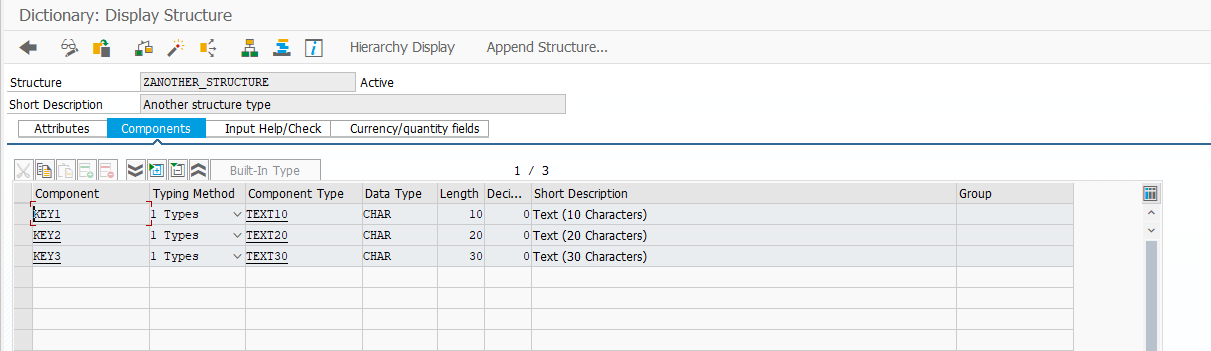
Structure type with different component names
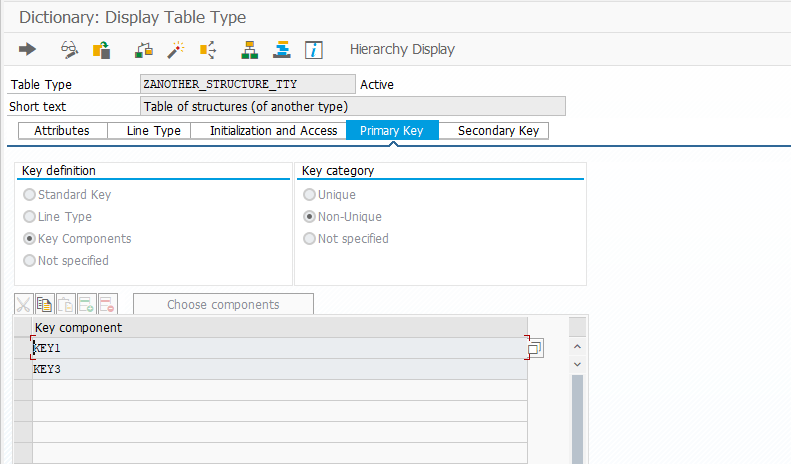
Table type for the new structure type
|
|
This makes a kind of sense, since two tables containing identical structures and ordered according to the same components (as far as the order of components in the structure is considered) will result in the same order of rows (excluding cases where multiple instances of the same key are allowed). Then again, even though the components are technically identical, their different naming would imply that the two structures probably do not represent exactly the same thing, which suggests that the two types should probably be incompatible.
The table key does not only determine table compatibility, but also the implicit sort order. In ABAP, you can sort a table without specifying the fields according to which the sort should happen:
|
|
The latter SORT statement sorts the table according to the table type primary keys, which would be A2 and B1 (contents of all character fields of the row concatenated) in the example. In this case, the result would be fairly sane.
Nevertheless, there is probably never a reason to use the implicit primary key for sorting: it is far more expressive and clear when the fields are written out when sorting a table. And, in cases where the key of a STANDARD table if empty, the SORT table statement will not actually even do anything. If the order of entries in a table really matters, it is probably better to use a SORTED table which will then always enforce the correct order, rather than rely on the programmer sorting the table after rows are manipulated.
Dangerous ABAP Statements
The craziest thing about the different ABAP table type types is that, depending on the type, only some table modification statements are safe to use.
For example, APPEND statement adds one or more new rows as the last row of the table. This works without issues when used with STANDARD tables, since elements can be freely added anywhere as there is no defined order, but will crash if used with SORTED tables:
|
|
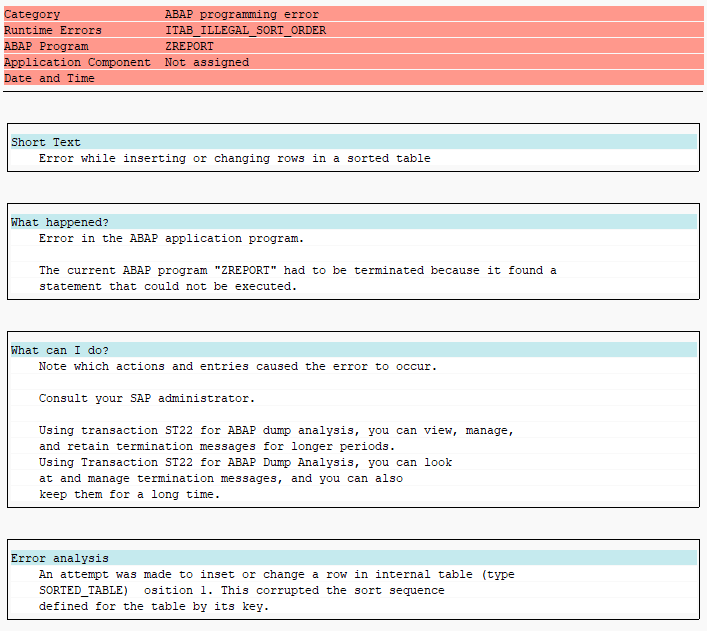
APPEND crashes when the order of rows is incorrect
INSERT statement works with all table types, except when trying to insert multiple rows with identical keys into a table with a unique key constraint:
|
|
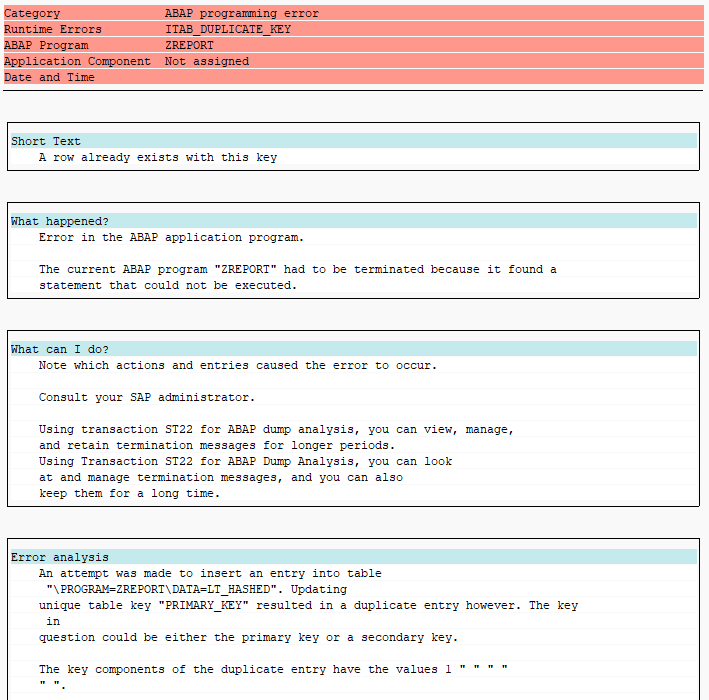
INSERT crashes when the operation would result in duplicate keys
Implicit conversion between table types can also crash for the same reason:
|
|
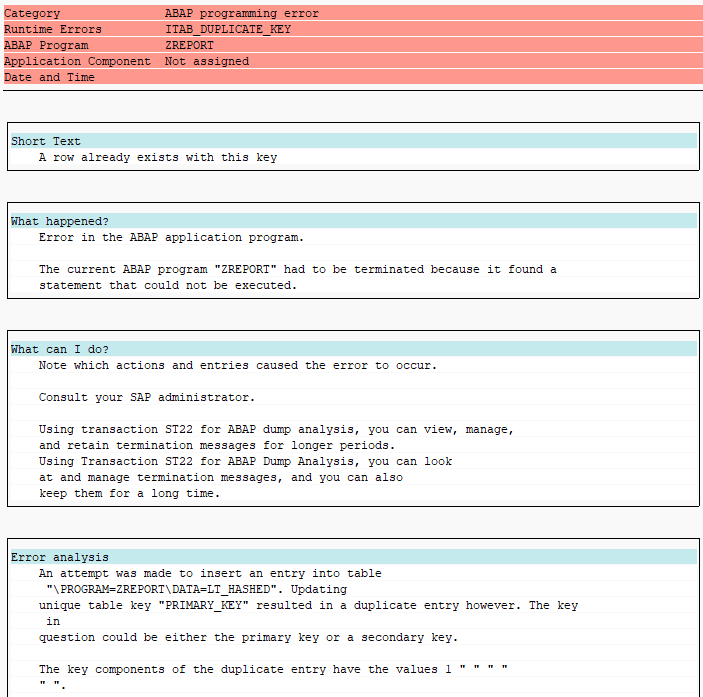
Conversion crashes when the operation would result in duplicate keys
Key fields are also protected from changes in SORTED and HASHED tables:
|
|
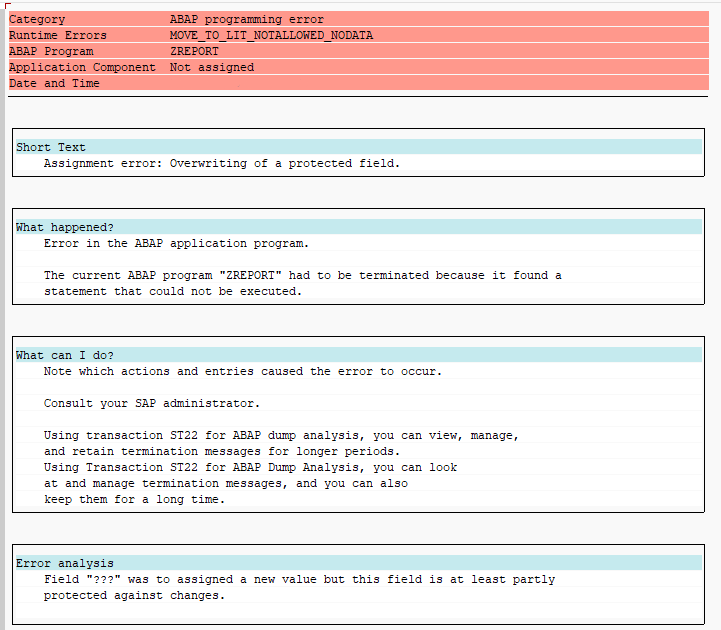
Key field are write-protected
Tables of Classes and Interfaces
Classes and interfaces add more interesting cases for table type (in)compatibility. A table of class instances is compatible with a table of interface instances if that class implements the interface:
|
|
Unfortunately this does not seem to work outside of classes:
|
|
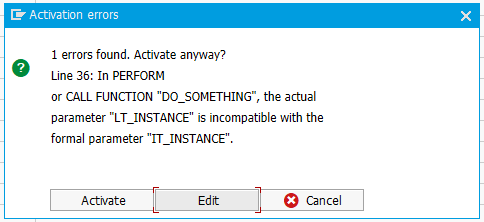
Table of class instances implementing the interface does not work
Generic Table Types
Some interesting things to note about the ABAP dictionary table type definition screenshots were the generic options for table type (“Index Table” and “Not specified”) and for table key (“Not Specified” for key definition and key category). These types of tables cannot be used when defining variables:
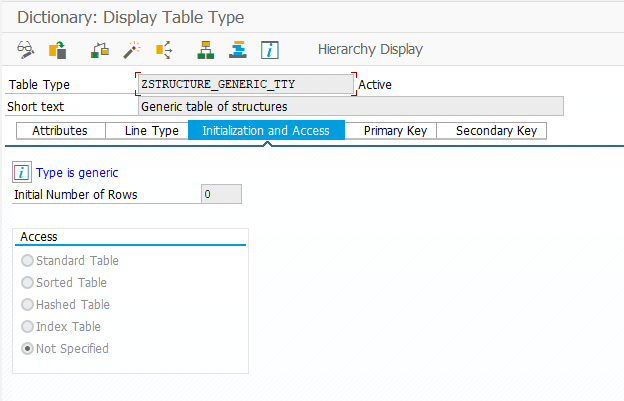
Generic table type
|
|
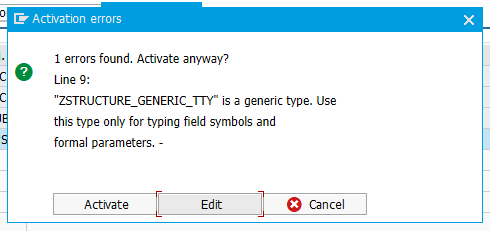
Generic table type error
Rather, these generic table types can be used to restrict allowed parameter types, without specifying exactly what type of table is expected. The most lenient table type (“Not Specified”) would just specify what sort of data the table contains, while allowing the actual type to be a STANDARD, SORTED or HASHED table. “Index Table” would only allow STANDARD and SORTED tables.
Leaving the key generic would allow different types of STANDARD, SORTED or HASHED tables to a be used as the actual parameter.
Of note is that the type definition STANDARD TABLE OF x stands for either a generic table definition (when used in a parameter, or rather, when used in a TYPES declaration), or a table type with an implicit standard key (when used in a variable definition, ie. when used in a DATA declaration):
|
|
Parameters can also be specified as a table of some kind without even specifying the type the table contains, but this is so generic as to be virtually useless and is only maybe useful in highly specific situations:
|
|
It is good to keep in mind that generic parameters always have the potential to transform type incompatibilities from compilation errors into runtime errors (previously mentioned in Function Modules, Methods and Type Safety). In the following example, the parameter type ty_index_table_of_zstructure allows for STANDARD and SORTED tables, whereas parameter type ty_std_table_of_zstructure explicity requires a STANDARD table with default key. The code compiles, because the generic parameter might contain the correct type of table, but will crash because the actual types are incompatible at runtime:
|
|
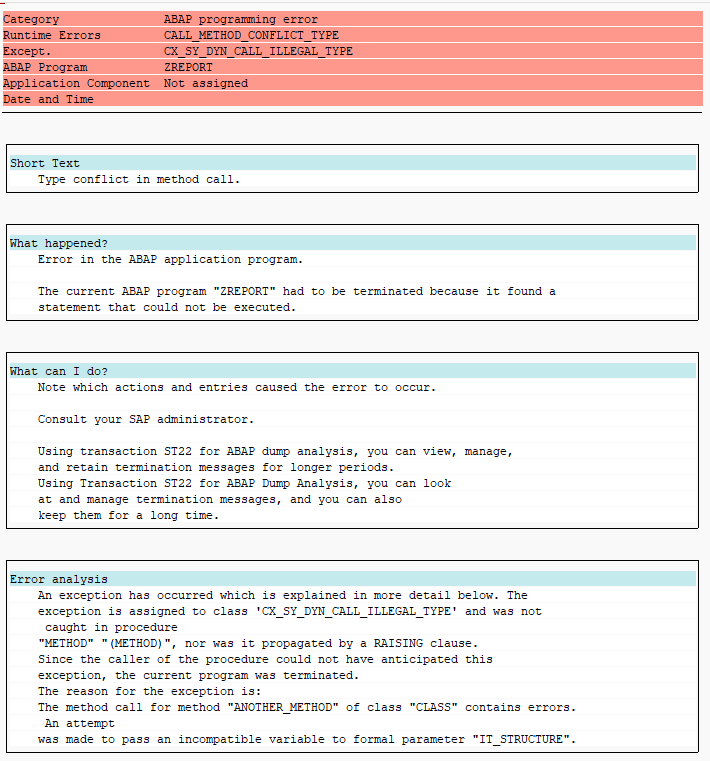
Generic type masks the actual parameter and crashes when executed
Implementing Sets
Although ABAP does not have built-in Set type, the most rudimentary operations can be easily simulated with a HASHED table:
|
|
Ranges
Ranges, AKA. Select-Options, are special tables that represent conditions for selecting data from the database. For example, if we wanted to select IDocs in some specific data range, we could use ranges to do this:
|
|
We could also use ranges to only select IDocs created on a specific date:
|
|
Ranges can represent many different sorts of conditions, and also combinations of these different condition types.
Type Inference
In recent versions of ABAP, table types can also be inferred in certain cases. This is especially useful when accessing the database:
|
|
Function Modules and TABLES Parameters
Another peculiarity of ABAP is that, in addition to USING, CHANGING, IMPORTING, EXPORTING and RETURNING parameters, there are also TABLES parameters:
|
|
I suspect there are two reasons for the existence of TABLES parameters:
- Tables in ABAP are value types, meaning that passing a table around requires copying it and all contained rows. Handling tables efficiently (= without unnecessary copying) as parameters may have required optimizations that were easier to implement when tables had their own parameters.
- Tables parameters allow for syntax where only the contained value needs to be specified, allowing for tables to be passed as parameters without having a global table type defined.
The first argument is obsolete, since IMPORTING and CHANGING (and also EXPORTING) parameters achieve similar performance:
|
|
|
|
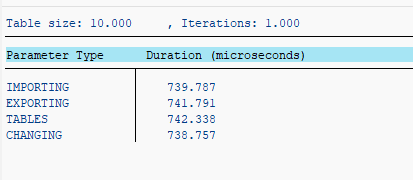
TABLES parameters are not especially faster or slower than others
The second argument still holds; passing tables using the other parameters requires a globally defined table type, whereas our TABLES parameter refers only to the contained type.
This introduces the following question: since we only the specify the contained type and not the table type, what sort of table is a TABLES parameter, actually. Can we pass a SORTED table into a TABLES parameter?
|
|
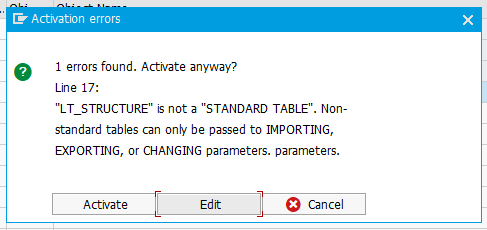
Clearly not ("parameters. parameters." is always a nice touch, though)
ABAP documentation also tells us that TABLES parameters are standard tables, but does not go into more detail. It also mentions that “Pass by value is not possible,” which aligns with my previous speculation about tables and performance optimizations:
Defines the table parameters t1 t2 … in the function module interface display in the source code of function modules. Table parameters are obsolete CHANGING parameters that are typed as standard tables with a header line. If an internal table without a header line or a table body is passed as an actual parameter to a formal parameter of this type, an empty local header line is generated in the function module. If an internal table with a header line is used as an actual parameter, both the table body and the header line are passed to the function module. Pass by value is not possible in formal parameters defined using TABLES.
Trying out different types of STANDARD tables inside and outside the function module gives us a bit more information:
|
|
So inside the function module, the TABLES parameters appears to be a STANDARD table with default key, as far as the ABAP compiler is concerned. This requirement, however, does not apply outside the function module:
|
|
This snippet compiles (obviously, since function module parameter types are not checked when compiled) and also executes without issues. So while the type of the table inside the function module appears to a STANDARD TABLE OF zstructure WITH DEFAULT KEY, we can actually use any sort of STANDARD table as the parameter.
So which is the actual type? The one we actually pass into the function module or the type that the TABLES parameter appears to be inside the function module?
|
|
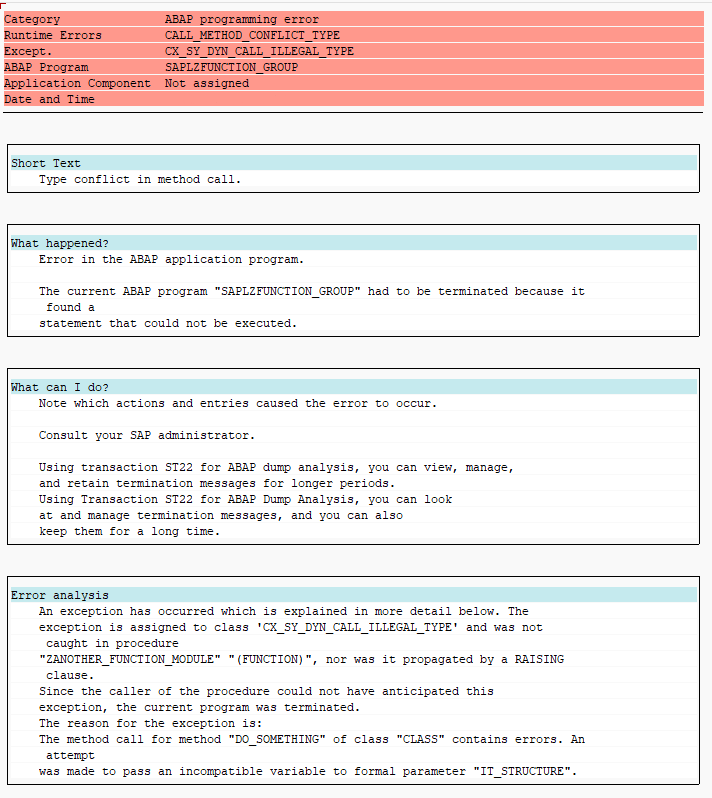
Function Module masks the actual type
At least when the function module is executed in the same session (function modules called via RFC may behave differently), the actual type is the table type that the caller used in the function module call. This is somewhat similar to cases where generic types mask type incompatibility which were mentioned earlier, but with a slight twist. Instead of the table inside the function module being a generic type which would be compatible with any STANDARD table parameter type, the TABLES parameter explicitly appears as a STANDARD TABLES OF x WITH DEFAULT KEY.
Clearly, a TABLES parameter can hide issues with incompatible types during compilation. Yet there’s also a sort-of solution on offer: given that any function module that compiles can only contain method calls that expect parameters typed STANDARD TABLE OF x (generic STANDARD table) or STANDARD TABLE OF x WITH DEFAULT KEY, using a table declared as DATA lt_table TYPE STANDARD TABLE OF x [WITH DEFAULT KEY] will always work, since any call inside the function module will have to work with a table of that type.
Some Final Thoughts
Although tables are fundamental building blocks that appear multiple times in most ABAP programs, they still hide details that one might not know about. For example, the fact that STANDARD TABLE OF x means different things in DATA vs. TYPES is easy to overlook, as is the exact type of a TABLES parameter.